CryptoDB
Non-Malleable Codes for Bounded Parallel-Time Tampering
| Authors: |
|
|---|---|
| Download: |
|
| Conference: | CRYPTO 2021 |
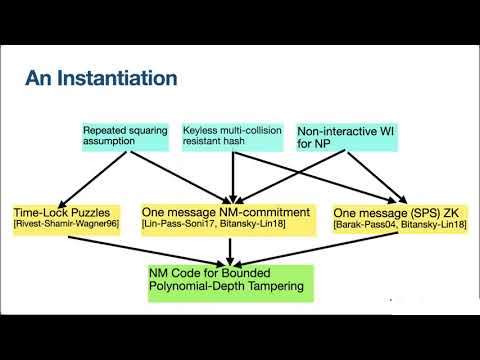
| Abstract: | Non-malleable codes allow one to encode data in such a way that once a codeword is being tampered with, the modified codeword is either an encoding of the original message, or a completely unrelated one. Since the introduction of this notion by Dziembowski, Pietrzak, and Wichs (ICS '10 and J. ACM '18), there has been a large body of works realizing such coding schemes secure against various classes of tampering functions. It is well known that there is no efficient non-malleable code secure against all polynomial size tampering functions. Nevertheless, no code which is non-malleable for \emph{bounded} polynomial size attackers is known and obtaining such a code has been a major open problem. We present the first construction of a non-malleable code secure against all polynomial size tampering functions that have {bounded} parallel time. This is an even larger class than all bounded polynomial size functions. In particular, this class includes all functions in non-uniform $\mathbf{NC}$ (and much more). Our construction is in the plain model (i.e., no trusted setup) and relies on several cryptographic assumptions such as keyless hash functions, time-lock puzzles, as well as other standard assumptions. Additionally, our construction has several appealing properties: the complexity of encoding is independent of the class of tampering functions and we can obtain (sub-)exponentially small error. |
Video from CRYPTO 2021
BibTeX
@inproceedings{crypto-2021-31194,
title={Non-Malleable Codes for Bounded Parallel-Time Tampering},
publisher={Springer-Verlag},
doi={10.1007/978-3-030-84252-9_18},
author={Dana Dachman-Soled and Ilan Komargodski and Rafael Pass},
year=2021
}