CryptoDB
Batch-OT with Optimal Rate
| Authors: |
|
|---|---|
| Download: | |
| Presentation: | Slides |
| Conference: | EUROCRYPT 2022 |
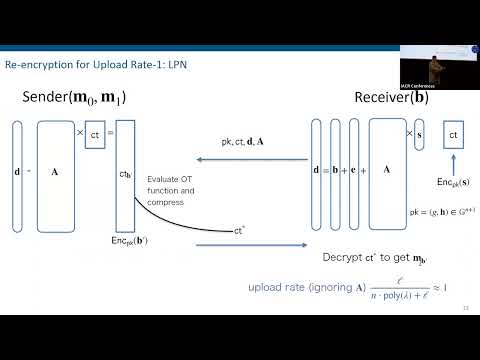
| Abstract: | We show that it is possible to perform |
Video from EUROCRYPT 2022
BibTeX
@inproceedings{eurocrypt-2022-31828,
title={Batch-OT with Optimal Rate},
publisher={Springer-Verlag},
author={Zvika Brakerski and Pedro Branco and Nico Döttling and Sihang Pu},
year=2022
}